Maximos, minimos y punto de inflexion

MAXIMOS, MINIMOS Y PUNTO DE INFLEXION

Como localizar puntos máximos y minimos :

la primer derivada igualándola a cero la cordenada Y se encuentra resolviendo la función

de X del vértice f´(x) = 0

Pendiente de una recta

PENDIENTE DE UNA RECTA

Es el cambio o diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta.

Fórmula:
M= delta Y / delta X

Ejemplo:

Hallar la pendiente de una recta que pasa porS(6,-4), T(2,-3)
M = Yb-Ya/Xb-Xa = 3+4/2-6 = -1.75
la pendiente es 1.75

Distancia entre dos puntos

DISTANCIA ENTRE DOS PUNTOS

La distancia entre dos puntos es la longitud del camino más corto entre ambos. es decir, la medición del grado de cercanía que existe entre los dos

Ejemplo:

Hallar las coordenadas del punto situado sobre el ejeY equidistante de los puntos M (5,5) y N (4,2).

Como el punto pedido P esta sovre el eje Y, y su abscisa es cero, su ordenada la designamos por Y, entonces P (0,y)

La distancia de P a M esla raiz 2 de (5-0) al cuadrado + (5,y) 2
y la de P a N esla raiz 2 de (4-o) 2 + (2-y) 2

Como ambas deven ser iguales:la raiz 2 de (5)2 + (5-y)2 es igual que la raiz cuadrada de (4)2 + (2-y) 2

Elevamos al cuadrado ambos miembros de la igualdad y efectuamos los cuadrados indicados quedando25+25-10y+(y)2 = 16+ 4 - 4y + (y)2candelando (y)2 y dejando en el primer miembro solamente los terminos en y-10+4y=16+4-25-25
los que nos lleva a Y=5
la respuesta es (0,5)

Regla de la Cadena

LA REGLA DE LA CADENA

La regla de la cadena es una fórmula para la derivada de la composición de dos funciones.
Tiene aplicaciones en el cálculo algebraico de derivadas cuando existe composición de funciones.
Descripción de la regla:
En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto a x puede ser computado como el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.

Funciones

FUNCIONES CUADRATICAS

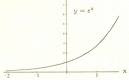
Una función cuadrática es toda función que pueda escribirse de la forma f(x) = a x2 + b x + c, donde a, b y c son números cualesquiera, con la condición de que a sea distinto de 0.

La función cuadrática más sencilla es f(x) = x2

FUNCION LINEAL

Consta de dos partes:
Estudio de la pendiente o inclinación de la línea en el plano.
.
Estudio de la ubicación de la línea en el plano de coordenadas.Estos son los dos elementos básicos para plantear la ecuación de una función lineal:
La fórmula de la función lineal es la siguiente:
y=mx+b

FUNCIONES POLINOMICAS

Una función polinómica es una combinación lineal de funciones potencias de base real y exponente natural.

Las funciones polinómicas son continuas e indefinidamente derivables en todo IR.

FUNCION RACIONAL

Una función racional es una función que se obtiene como cociente de dos funciones polinómicas.Esta definida en todo IR excepto en los puntos donde el denominador se anula. En su dominio de definición, las funciones racionales son continuas e indefinidamente derivables.

FUNCION LOGARITMICA

Se llama función logarítmica a la función real de variable real

FUNCION EXPONENCIAL

Sea un número real positivo. La función que a cada número real x le hace corresponder la potencia se llama función exponencial de base a y exponente x.
Como para todo ,la función exponencial es una función de en .

Derivada...

LA DERIVADA DEL PRODUCTO

La derivada del producto de dos funciones es igual al primer factor por la derivada del segundo más el segundo factor por la derivada del primero.La derivada del producto de una constante por una función es igual al producto de la constante por la derivada de la función.Aunque dada la ecuación de una función es posible obtener su respectiva función derivada utilizando la definición, para algunas funciones este procedimiento resulta sumamente tedioso. Surge entonces la necesidad de simplificar este proceso, lo cual puede lograrse al estudiar los teoremas sobre derivadas.

DERIVADA EN RADICALES

El n-ésimo radical o raíz de un número a, que es el número cuya n-ésima potencia es a (ver también raíz cuadrada);as propiedades, entre ellas:
raíz de una raíz, raíz de una potencia, simplificación de radicales, ampliación de radicales, raíz de un producto, raíz de un cociente, suma de radicales, reducción a índice común, racionalización de denominadores, cociente de radicales, cociente de radicales de diferentes índices, radicales semejantes y no semejantes, adicción y sustracción entre radicales semejantes y no semejantes, con sus respectivos ejemplos.
Así mismo alcanzar las expectativas esperadas en la materia, de igual manera aumentar conocimientos en el área de matemática.

La derivada

LA DERIVADA

La derivada de una función en un punto representa el valor de la pendiente de la recta tangente en dicho punto. La pendiente está dada por la tangente del ángulo que forma la recta tangente a la curva (función) con el eje de las abscisas, en ese punto.La derivada de una función mide el coeficiente de variación de dicha función. Es decir, provee una formulación matemática de la noción del coeficiente de cambio. El coeficiente de cambio indica lo rápido que crece (o decrece) una función en un punto (razón de cambio promedio) respecto del eje x\, de un plano cartesiano de dos dimensiones. Por ejemplo, si tomamos la velocidad de un móvil, su coeficiente es la aceleración, la cual mide cuánto cambia la velocidad en un tiempo dado.

Circunferencia

LA CIRCUNFERENCIA

La CircunferenciaLa circunferencia es el lugar geométrico de todos los puntos en el plano P (x, y) que son equidistantes de un punto fijo.EL punto fijo es el centro de la circunferencia y cualquier segmento de recta cuyos extremos sean un punto cualquiera de la misma y su centro se llama radio

La ecuación ordinaria o reducida de la circunferencia es:
(x - h)2 + (y - k)2 = r2
Quedando: x2 + y2 = 25
El centro se representa:C (h , k) o (0 , 0)

Funciones Conicas

SECCIONES CONICAS

Las secciones cónicas ,son las figuras geométricas , que se obtienen cuando se intersecan un cono circular recto de dos mantos con un plano.

Ejemplo de secciones cónicas:

ELIPSE

Si un plano corta todo un manto del cono y no es perpendicular al eje de dicho cono, entonces la curva formada por la intersección se llama eclipse.

LA PARABOLA

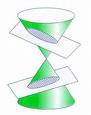
Si un plano corta a uno de los mantos de un cono pero no lo cruza, y además no tiene contacto con el otro, entonces la curva formada por la intersección se llama parábola.
Si continuamos inclinando el plano de modo que sea oblicuo con el eje y que sea paralelo a una generatriz resulta una parábola.